
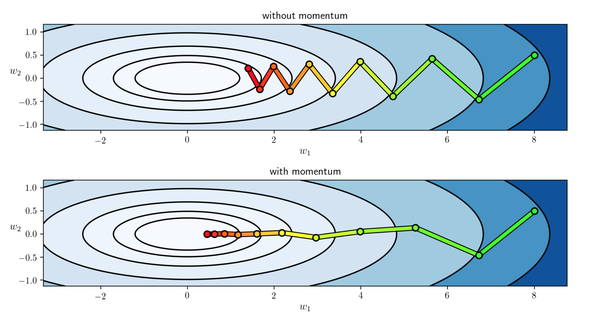
Finally \gamma \in (0,1] determines for how many iterations the previous gradients are incorporated into the current update. The learning rate \alpha is as described above, although when using momentum \alpha may need to be smaller since the magnitude of the gradient will be larger. In the above equation v is the current velocity vector which is of the same dimension as the parameter vector \theta.

\theta = \theta - \alpha \nabla_\theta J(\theta x^) \\
GRADIENT DESCENT ALGORITHM UPDATE
Stochastic Gradient Descent (SGD) simply does away with the expectation in the update and computes the gradient of the parameters using only a single or a few training examples. If instead one takes steps proportional to the. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient (or of the approximate gradient) of the function at the current point.
GRADIENT DESCENT ALGORITHM FULL
Where the expectation in the above equation is approximated by evaluating the cost and gradient over the full training set. Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function. The standard gradient descent algorithm updates the parameters \theta of the objective J(\theta) as, SGD can overcome this cost and still lead to fast convergence. The use of SGD In the neural network setting is motivated by the high cost of running back propagation over the full training set. Stochastic Gradient Descent (SGD) addresses both of these issues by following the negative gradient of the objective after seeing only a single or a few training examples. Another issue with batch optimization methods is that they don’t give an easy way to incorporate new data in an ‘online’ setting. However, often in practice computing the cost and gradient for the entire training set can be very slow and sometimes intractable on a single machine if the dataset is too big to fit in main memory. minFunc) because they have very few hyper-parameters to tune. They are also straight forward to get working provided a good off the shelf implementation (e.g. Batch methods, such as limited memory BFGS, which use the full training set to compute the next update to parameters at each iteration tend to converge very well to local optima.


 0 kommentar(er)
0 kommentar(er)
